Rumus Segitiga Siku-siku: Penjelasan Lengkap dan Contoh Penggunaan

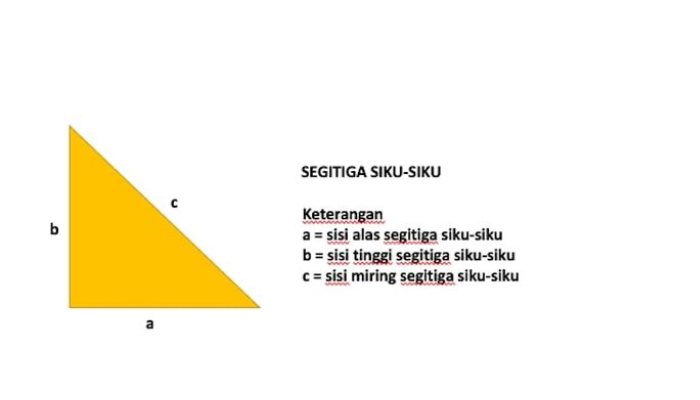
Segitiga siku-siku adalah salah satu bentuk segitiga yang memiliki satu sudut yang besarnya 90 derajat. Rumus segitiga siku-siku adalah kumpulan perhitungan yang digunakan untuk menemukan panjang sisi-sisi segitiga serta luas dan kelilingnya. Dalam artikel ini, kita akan membahas rumus-rumus yang terkait dengan segitiga siku-siku beserta contoh penggunaannya.

Sifat-sifat Segitiga Siku-siku

Sebelum kita masuk ke rumus-rumusnya, mari kita tinjau terlebih dahulu beberapa sifat penting dari segitiga siku-siku:

• Segitiga siku-siku memiliki satu sudut yang besar 90 derajat, yang disebut sudut siku-siku.
• Sisi yang berlawanan dengan sudut siku-siku disebut sebagai sisi miring atau hipotenusa.
• Sisi yang menyusun sudut siku-siku disebut sebagai sisi tegak atau kaki tegak.
• Sisi lainnya disebut sebagai sisi alas atau kaki alas.

Rumus Segitiga Siku-siku

Rumus-rumus segitiga siku-siku, terutama Teorema Pythagoras, sangat berguna dalam memecahkan berbagai masalah matematika dan fisika yang melibatkan segitiga siku-siku. Dengan memahami rumus-rumus ini, kita dapat dengan mudah menghitung panjang sisi-sisi segitiga, luasnya, dan melakukan berbagai aplikasi lainnya.

Rumus Pythagoras

Rumus Pythagoras adalah salah satu konsep paling fundamental dalam matematika yang digunakan untuk menghitung panjang sisi miring (hipotenusa) sebuah segitiga siku-siku. Rumusnya adalah:

c² = a² + b²

di mana:

c adalah panjang sisi miring (hipotenusa),

a dan b adalah panjang sisi-sisi lainnya (kaki tegak dan kaki alas).

Rumus Keliling

Untuk menghitung keliling segitiga siku-siku, kita dapat menggunakan rumus:

K = a + b + c

K adalah keliling segitiga

a, b, dan c adalah panjang sisi-sisi segitiga.

Rumus Luas

Rumus untuk menghitung luas segitiga siku-siku adalah:

A = ½ x a x b

Dimana : 

A adalah luas segitiga,

a dan b adalah panjang sisi-sisi segitiga yang bersilangan di sudut siku-siku.

Contoh Penggunaan Rumus

Mari kita lihat contoh penggunaan rumus-rumus segitiga siku-siku dalam situasi nyata:

Menghitung Panjang Sisi Miring

Diberikan sebuah segitiga siku-siku dengan panjang sisi tegak a=3 dan panjang sisi alas b=4, kita ingin mencari panjang sisi miring (hipotenusa) c. Menggunakan rumus Pythagoras:

c² = 3² + 4²

c² = 9 + 16

c² = 25

c² = √25 = 5

Jadi, panjang sisi miring segitiga tersebut adalah 5 satuan

Menghitung Luas Segitiga

Misalkan kita memiliki segitiga siku-siku dengan panjang sisi tegak a=6 dan panjang sisi alas b=8. Untuk menghitung luas segitiga, kita gunakan rumus luas:

A = ½ x 6 x 8 = 24

Jadi, luas segitiga tersebut adalah 24 satuan persegi.

Kesimpulan

Rumus segitiga siku-siku, termasuk rumus Pythagoras, rumus keliling, dan rumus luas, adalah alat penting dalam matematika yang digunakan untuk menghitung berbagai aspek segitiga siku-siku. Dengan memahami dan menguasai rumus-rumus ini, kita dapat dengan mudah menyelesaikan berbagai masalah geometri yang melibatkan segitiga siku-siku.