Rumus Rumus Luas Permukaan Bola

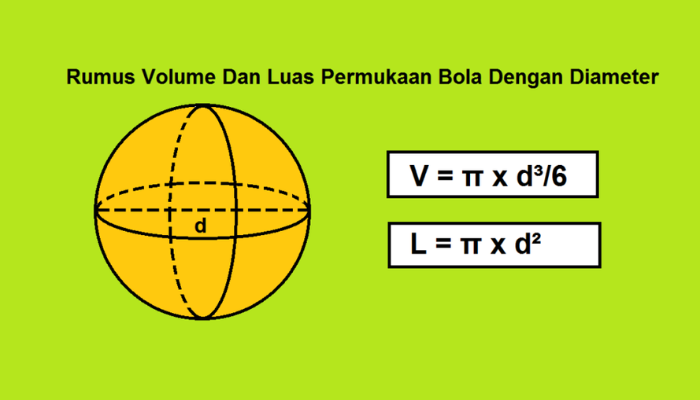
Rumus luas permukaan bola adalah alat matematika yang sederhana namun kuat untuk memahami dan mengukur sifat-sifat geometris dari bentuk sferis ini. Dengan menggunakan rumus ini, kita dapat dengan mudah menghitung luas permukaan bola dan menerapkannya dalam berbagai konteks dalam ilmu pengetahuan, teknik, dan kehidupan sehari-hari. Dalam dunia matematika, bola adalah salah satu bentuk geometris yang paling sederhana namun penuh dengan keindahan dan keunikan. Di balik keindahannya, ada rumus sederhana yang mengungkapkan luas permukaan bola, suatu konsep yang penting dalam berbagai bidang ilmu pengetahuan. Mari kita eksplorasi lebih dalam tentang rumus ini.

Konsep Dasar Rumus Bola

Sebelum kita membahas rumus luas permukaan bola, mari kita pahami terlebih dahulu apa itu bola. Bola adalah bentuk tiga dimensi yang terdiri dari semua titik yang memiliki jarak yang sama dari pusatnya. Ini berarti setiap titik di permukaan bola berjarak sama dari pusatnya, menciptakan simetri yang sempurna dalam bentuknya.

Rumus Luas Permukaan Bola

Rumus matematika yang digunakan untuk menghitung luas permukaan bola adalah:

Luas Permukaan Bola = 4πr²

Di sini:

• π adalah konstanta matematis yang mendefinisikan perbandingan keliling lingkaran dengan diameternya, dengan nilai kira-kira 3.14159.
• r² adalah jari-jari bola.

Rumus ini secara elegan mengungkapkan bahwa luas permukaan bola adalah empat kali luas lingkaran dengan jari-jari yang sama dengan jari-jari bola. Intuitifnya, kita dapat membayangkan bola sebagai tumpukan lingkaran tak terbatas dengan jari-jari yang semuanya sama.

Contoh Penerapan

Misalnya, jika kita memiliki bola dengan jari-jari sepanjang 5 cm, kita dapat menggunakan rumus ini untuk menghitung luas permukaannya:

LuasPermukaanBola = 4π(5)²

Kesimpulan

Rumus Luas Permukaan Bola adalah alat matematika yang sederhana namun kuat yang memungkinkan kita untuk memahami sifat-sifat geometris dari bentuk ini. Dengan menggunakan rumus ini, kita dapat dengan mudah menghitung luas permukaan bola dalam berbagai konteks, mulai dari ilmu fisika hingga matematika murni. Ini adalah salah satu contoh kekuatan matematika dalam menggambarkan dan memahami dunia di sekitar kita.