Rumus Luas Kubus: Menghitung Total Area Permukaan Kubus

Kubus adalah salah satu bentuk geometri tiga dimensi yang paling sederhana, tetapi memiliki berbagai aplikasi dalam berbagai bidang, termasuk matematika, fisika, dan rekayasa. Salah satu konsep dasar yang penting dalam memahami kubus adalah rumus untuk menghitung luas permukaannya. Dalam artikel ini, kita akan menjelaskan secara detail tentang rumus luas kubus, bagaimana menggunakannya, dan mengapa rumus ini penting dalam konteks matematika dan dunia nyata.

Konsep Dasar Kubus

Sebelum kita membahas rumus luas kubus, mari kita pahami terlebih dahulu konsep dasar tentang kubus:

• Definisi Kubus: Kubus adalah bentuk tiga dimensi yang memiliki enam sisi persegi dengan panjang sisi yang sama.
• Sifat Kubus: Setiap sisi kubus memiliki panjang sisi yang sama, dan setiap sudut dalam kubus adalah sudut siku-siku.
• Elemen Kubus: Beberapa elemen penting dari kubus meliputi panjang sisi s, luas permukaan, volume, dan diagonal.

Rumus Luas Kubus

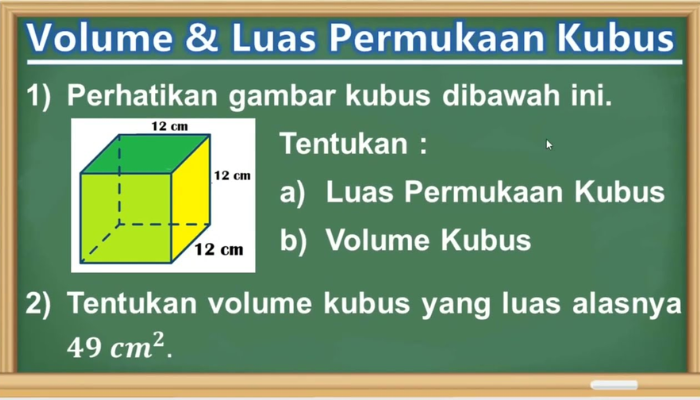
Luas kubus adalah ukuran dari total area permukaan luarnya. Karena setiap sisi kubus adalah persegi dengan panjang sisi yang sama, rumus untuk menghitung luas permukaan kubus adalah:

L kubus = 6 x s²

Dimana :

L kubus adalah luas permukaan kubus

s adalah panjang sisi kubus

Penerapan Praktis Rumus Luas Kubus

Rumus luas kubus memiliki berbagai aplikasi dalam kehidupan sehari-hari dan berbagai bidang ilmu, termasuk:

• Matematika: Dalam matematika, rumus ini digunakan untuk mengajarkan konsep geometri tiga dimensi dan perhitungan luas permukaan.
• Arsitektur: Dalam arsitektur, rumus luas kubus digunakan dalam perencanaan bangunan, perumahan, dan desain interior.
• Fisika: Dalam fisika, konsep kubus dan rumus luasnya sering muncul dalam pemodelan dan perhitungan volume benda padat.
• Teknik: Dalam rekayasa, pemahaman tentang luas kubus penting dalam desain dan perhitungan struktur bangunan dan perangkat mekanis.

Kesimpulan

Rumus Luas Kubus adalah alat matematika yang penting untuk menghitung total area permukaan luar dari kubus. Dengan pemahaman yang baik tentang rumus ini, kita dapat menerapkannya dalam berbagai konteks, dari matematika murni hingga aplikasi praktis dalam dunia nyata. Rumus luas kubus membantu kita memahami sifat dan karakteristik geometri tiga dimensi yang sederhana tetapi penting ini.